

The object of this booklet is to describe the principles of magnetic core memories in a simple and clear way. It explains why cores with a rectangular hysteresis loop are used, the principle of coincident currents and the way a decimal number is stored and extracted from the memory.
The booklet was originally published for customers of the Industrial Electronics Division of Mullard Limited.
The essential functions of a brain, whether it be that of a human being or the so-called ‘electronic brain’ which is being so widely adopted for computers (calculating apparatus), in automatic control systems, and for book-keeping and accountancy installations, are the following:
The main differences between a human brain and an artificial ‘electronic’ brain are in the manner in which information is applied, stored, recalled and utilised.
In the human brain, information is received via the senses – sight, hearing, touch, smell and taste. The electronic brain, however, receives information only in the form of electrical impulses, meaningless in themselves, but having specific significance when applied according to a suitable code. This coding, of course, must be performed by an external agency – human, mechanical or electrical, or by a combination of these. Examples of such agencies are perforated-card systems, light-sensitive devices, and temperature-sensitive devices.
The mechanism of information storage in the human brain is not precisely known, but there is good evidence that it is partly, if not entirely, electro-chemical. In ‘electronic’ brains information is usually stored in the form of different conditions of magnetisation or of electrical charge, in a number of ‘memory elements’.
The recall of previous impressions or stored information in the case of a human brain may be a simple act of will, or imagination, or the reception of some similar or related impression – for example, a particular scent may recall memories of a pleasant evening spent with a girl who used the same perfume. In the case of an electronic brain, however, the recall of stored information can result only from the application of further coded impulses, again controlled by human agency.
Initiation of action in the case of a human brain may again be an act of will, or it may be semi-automatic – as when a feeling of burning causes one to withdraw one’s hand from a hot tea-pot handle – or it may be entirely automatic, such as the beating of the heart. With electronic brains, however, initiation of action occurs only as a result of a specially applied coded signal. It will thus be clear that the potentialities of the electronic brain are in many respects subject to severe limitations compared with the potentialities of the human brain. In particular, the electronic brain possesses no will power, no imagination, no sentimentality, and no discretionary power. On the other hand, a given code signal will always result in the storage of the same information, or the recall and utilisation of the same selection of the stored material. Furthermore, unless some failure occurs in the electrical system, an electronic brain cannot make mistakes due to incorrect calculation of lack of judgment.
The limitations of the electronic brain stem from the fact that, whereas the human brain details, in the main, with impressions, sensations, facts and ideas, the electronic brain deals only with numbers – and coded numbers at that.
This booklet is concerned with the particular form of artificial memory equipment which operates on the principle of patterns of different conditions of magnetisation in a complex of magnetic elements.
We have said that an artificial brain can deal only with numbers. Of course the human brain can also deal with numbers, but not exclusively with numbers. Human beings, at least in most civilised countries, use for the purposes of recording and calculation what is known as the decimal system of notation, in which any quantity or number can be represented by an appropriate combination of figures or symbols, of which there are ten kinds – the figures 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
Most magnetic memories operate on what is known as the ‘binary’ notation, in which quantities (numbers) are represented by suitable arrangements of symbols of two kinds only, namely 0 and 1. Not only quantities, but also letters, words or commands can be represented by means of the binary code. It will be shown later* that all numbers between 0 and 9 in the decimal notation can be denoted in the binary code by various combinations of 0 and 1 distributed over four magnetic elements. Larger quantities, of course, require a larger number of elements.
* See section ‘Relation between the Decimal and Binary Codes’.
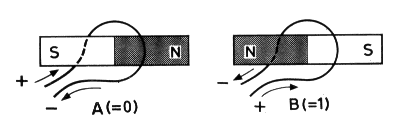
The first step in developing a magnetic memory to operate on the binary scale of notation was to select two magnetic conditions which might represent the symbols 0 and 1. The conditions selected are the direction in which each magnetic element is magnetised. It is well known that a piece of so-called magnetic material, that is to say a piece of magnetisable material, e.g. iron or the iron compound known as ‘ferroxcube’, can be magnetised in either of two opposite directions, as indicated diagrammatically in Fig. 1.

A piece of magnetisable material when magnetised in the direction shown at A might represent the symbol 0, and when magnetised in the direction shown at B, the symbol 1. It is also well known that a piece of magnetisable material can be magnetised only by applying a magnetising force, technically termed a magnetising field or magnetic field. One way of applying a magnetic field is by surrounding the magnetisable material by a coil or loop wire carrying an electric current. The direction of the magnetisation is determined by the direction of the current, as indicated in Fig. 2, where the direction of the current is indicated by arrows.
Thus, if the current flows in the direction of the arrows (as shown at A), the material will be magnetised in the direction previously selected to represent the symbol 0, and if the current flows in the direction indicated at B, the direction of the magnetisation will be that selected to represent the symbol 1.
However, immediately after the magnetising field is removed by switching off the current, part of the magnetism which has been ‘induced’ in the material disappears, and only a portion, known as the ‘remanent magnetism’ is retained. With most magnetisable materials the magnetism which remains when the current is switched off is very much less than that existing in the material while the current is flowing.
The relationship between the direction and strength of the resultant magnetism (denoted B) and the direction and strength of the magnetising force (denoted H) is shown in the graphs termed ‘hysteresis loops’, reproduced in Fig. 3. For most magnetic materials this graph is of the form indicated in Fig. 3a, and it is seen that a magnetising force of +HP results in a degree of magnetism equal to +BP, but when the magnetising force is removed the remanent magnetism is only +BR. Similarly, a magnetising force -HP results in a degree of magnetisation -BP and when the magnetising force is removed the remanent magnetism is only -BR.
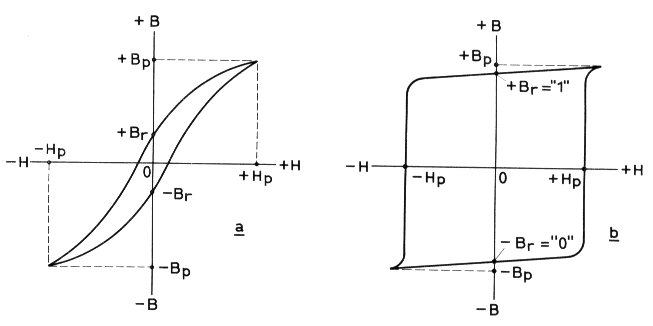
Because, in magnetic memories, stored information takes the form of the remanent magnetism in one or other of the two states +BR and -BR, one of them representing ‘0’ and the other representing ‘1’, it is important that there should be a very definite difference between these two states. To ensure this, a material is therefore chosen in which the value of BR does not differ greatly from the value of BP. Such a material is ‘ferroxcube 6’, the magnetisation curve of which is of the form indicated in Fig. 3b. In actual practice, and for reasons which will appear later, straight bars of iron and complete loops or coils of wire are not used in magnetic memories. Instead, rings of the iron compound ‘ferroxcube 6’ are employed, and in place of loops, straight wires are threaded through these rings.

So far we have discussed, in a very simple way, the principles on which a magnetic memory is based. It is now necessary to consider certain aspects of the subject from a more technical angle, and in particular explain more fully why the material ‘ferroxcube 6’ has been selected for use in the equipment to be described.
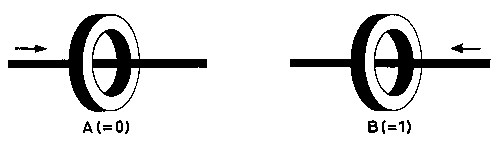
It has been shown that the direction of the magnetisation of a particular ring element is determined by the direction of the current flowing through the wire on which the ring is threaded (see Fig. 4). It should also be understood that the extent to which a ring is magnetised is proportional to the strength of the current flowing through the wire, in other words to the strength of the magnetising field.
The relationship between the direction and strength of the resultant magnetisation (B) and the direction and strength of the magnetising force (H), for the material ferroxcube 6 is shown once more in the graphs reproduced in Fig. 5.
Depending upon what has previously happened by way of applying a magnetising force H, a ring core, when no current is flowing in the wire threaded through it, will, due to the special form of the hysteresis loop, be in one of two magnetic conditions: it will either be magnetised in the direction we will call ‘+’, to an extent +Br, or in the direction we will call ‘-’ to an extent -Br. The condition +Br is used to represent the symbol ‘1’, and the condition -Br to represent the symbol ‘0’. In order to change the magnetic condition of the ring core from +Br to -Br, or vice versa, a current corresponding to a magnetising force H must pass through the wire. In actual practice, where a number of wires pass through each ring core, the algebraic sum of the currents in all the wires must be equivalent to a magnetising force H.
For example, imagine that a particular ring is in the condition +Br, representing the symbol 1. If a current equivalent to a field of -H is now passed through the wire (see lowest horizontal block in Fig. 5b), the magnetisation will be reversed, the condition changing to that corresponding to point P on the graph. When the current ceases (H becoming zero) the strength of the magnetisation will fall to the value marked -Br, that is to say the ring will be in the condition representing the symbol 0.
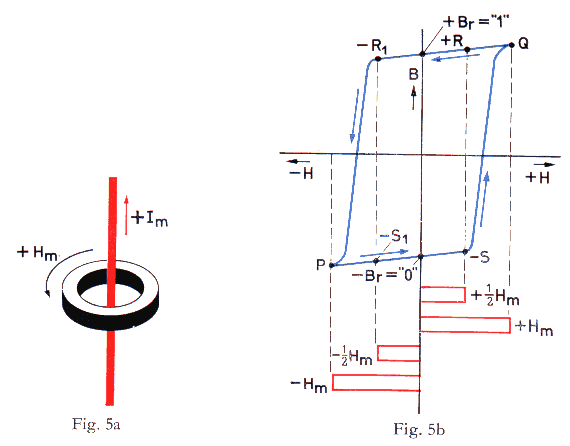
Similarly, if the ring core is originally in the condition -Br, the application of a current pulse corresponding to a magnetising force of +H will change the magnetisation to the point Q on the graph and, on cessation of the current, the magnetisation will drop to the value +Br.
Again, because of the rectangular form of the hysteresis loop, the application of a current pulse corresponding to a magnetising force of ½H in either direction will make no permanent change in the direction of the magnetisation. If the core is in the condition +Br, the application of a magnetising field of ½H will temporarily drive the magnetisation either to the value represented by +R on the graph or to the value represented by -R1, and on cessation of the current the magnetisation will return to the value +Br.
Similarly, if the core is in the condition -Br, the application of a magnetising field of ½H will temporarily drive the magnetisation either to the value represented by -S or to the value represented by -S1. On cessation of the current the magnetisation will again return to -Br.
The above effects are due to the rectangular form of the hysteresis loop, of the special grade of ferroxcube known as ‘ferroxcube 6’.
Fig. 6 is a sketch of a single ring core in the position in which it is mounted in a complete magnetic memory.
It consists of a ring of the magnetisable material ‘ferroxcube 6’ mounted at an angle of 45° and, threaded through it, four wires: one vertical wire termed the Y-wire, two horizontal wires termed the X- and Z-wire respectively, and one diagonal wire termed the S-wire.
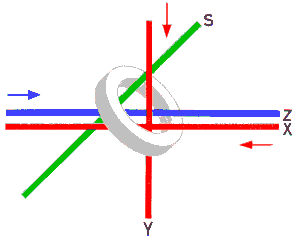
The arrow-heads drawn parallel to the X- and Y-wires indicate what we will consider as the ‘+’ direction for currents flowing in these wires. In operation, only current pulses corresponding to a field of either +½H or -½H are allowed to flow in the X- and Y-wires. If, therefore, the ring core is in the condition +Br, it will change to the -Br condition only if current pulses, each of which corresponding to a magnetising field of -½H, are sent simultaneously through both the X-wire and the Y-wire. Similarly, if the ring core is in the condition -Br it will change to the +Br condition only if current pulses corresponding to a total magnetic field of +H are sent simultaneously through the X- and the Y-wires.
It should be mentioned in passing that, just as currents passed through the X- and Y-wires can change the direction of the magnetisation of the ring, so does a change in magnetisation of the ring produce an electrical force, termed an ‘electro-motive force’ in the S-wire, capable of causing a current pulse to flow in that wire. It is this effect which is employed to ‘read out’ or recall the information stored in the memory.
The functions of the Z- and S-wires will be described more fully in a later section.

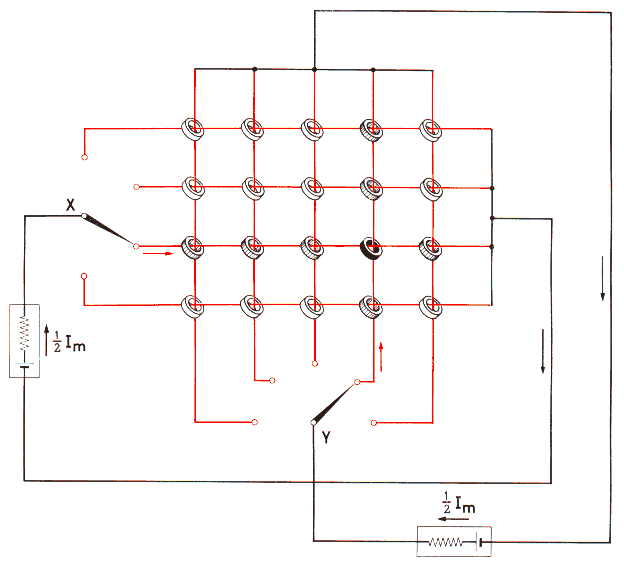
A complete magnetic core memory consists of a number of ring cores of the type described in the previous section, arranged in horizontal rows and vertical columns. Such an arrangement is shown in Fig. 7, in which, for the sake of simplicity, only the X- and Y-wires are indicated.
The complete set as illustrated is called a ‘memory plane’ or ‘matrix plane’ and in actual installations it would have many more than the 20 cores shown in the diagram. A small memory would have four such planes, stacked one above the other; larger memories have stacks of up to 100 planes.
It is seen that switches are provided whereby current pulses can be sent through the X-wire threaded through any selected horizontal row of ring core elements, and through the Y-wire threaded through any selected vertical column of elements. In practice, these switches consist of external devices, such as punched-card systems, for example.
The operation of a single memory plane can be simply understood by remembering that, at any given time, each of the ring cores is either in the condition 0 or in the condition 1. If, with the switches in the positions shown in Fig. 7, a current pulse corresponding to a magnetising field of +½H* is passed through the Y-wire of the fourth column from the left as indicated by the position of switch Y, and a similar current is at the same time passed through the X-wire of the third row from the top as indicated by the position of switch X, only the one core, situated at the point where the fourth column and the third row cross each other (shown in black in the diagram) will be subjected to the full magnetising field of (½H) + (½H) = +H. If that core was originally in the condition 0 it will immediately change to condition 1. If, however, it was originally in condition 1 it will remain in that condition.
*) In the following to be referred to as ½Im.
All the other ring cores in the fourth column and the third row will receive only the +½Im pulses and will not change their condition. These so-called half-selected cores are drawn with hatched shading. All the other cores in the memory plane receive no pulses and, evidently, they do not change their condition. It will also be clear that if -½Im pulses were passed through the same X- and Y-wires the selected core would, if originally in the 1 condition, change to the 0 condition or, if originally in the 0 condition, will remain in that condition.
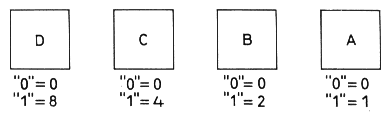
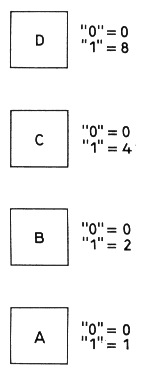
It was stated earlier that any of the ten symbols 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 of the decimal notation can be represented in the binary code by different combinations of the conditions 0 and 1 in a group of four elements. This can be simply explained by reference to Fig. 8 which shows the four elements.

Any element in the condition 0 is considered as equivalent to the decimal symbol 0. An element in condition 1 corresponds to the decimal symbol 1, 2, 4 or 8 according to its position in the group. In mathematical terms, the elements themselves, reading from right to left in Fig. 8, when in the 1 condition correspond to 20(=1), 21(=2), 22(=4) and 23(=8). In the 0 condition any element corresponds to 0, as previously stated. The actual decimal digit represented by a group of four elements is obtained by adding the four decimal symbols which the four elements represent.
The table below indicates how any decimal digit (0 to 9) can be expressed in the binary code with four elements (‘bits’).
| decimal digit |
binary code |
|---|---|
| 0 = 0·23 + 0·22 + 0·21 + 0·20 = | 0000 |
| 1 = 0·23 + 0·22 + 0·21 + 1·20 = | 0001 |
| 2 = 0·23 + 0·22 + 1·21 + 0·20 = | 0010 |
| 3 = 0·23 + 0·22 + 1·21 + 1·20 = | 0011 |
| 4 = 0·23 + 1·22 + 0·21 + 0·20 = | 0100 |
| 5 = 0·23 + 1·22 + 0·21 + 1·20 = | 0101 |
| 6 = 0·23 + 1·22 + 1·21 + 0·20 = | 0110 |
| 7 = 0·23 + 1·22 + 1·21 + 1·20 = | 0111 |
| 8 = 1·23 + 0·22 + 0·21 + 0·20 = | 1000 |
| 9 = 1·23 + 0·22 + 0·21 + 1·20 = | 1001 |
In a magnetic memory, the four elements required to represent a decimal digit are not mounted side by side as in Fig. 8, but are stacked one above another as shown in Fig. 9.
Here, reading upward from the lowest element (A) in the stack, elements in the 1 condition will represent 1, 2, 4 and 8. These four elements occupy corresponding positions in four matrix planes. It is important to remember that in order to store decimal numbers in the binary code a memory requires at least four matrix planes.
The X- and Y-wires of the stack of four elements are so connected that one X-pulse and one Y-pulse will influence all four elements required to represent a decimal symbol.

Fig. 10 represents the bottom left-hand corner of each plane of a stack of four matrix planes, only three core elements being shown for the sake of simplicity.
In this diagram, cores which are in the 1 condition are shown in black; cores in the 0 condition in white.
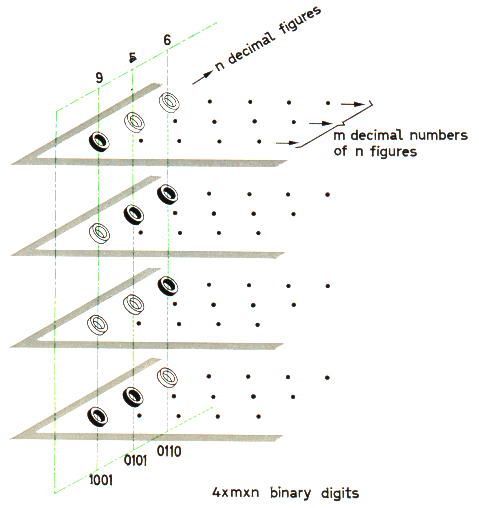
It will be seen that the cores in located at the extreme corners of the four matrix planes are in the conditions 1, 0, 0 and 1, reading upward from the bottom. According to the table, this sequence corresponds to (1 + 0 + 0 + 8) = 9 in the decimal notation.
Now it is usually required to store numbers consisting of more than one digit, and this is done by employing further stacks of four cores. This is also indicated in Fig. 10, where the first stack of four cores represents the digit 9 as already explained, while the cores in the next stack are in the conditions 1, 0, 1, 0, corresponding to (1 + 0 + 4 + 0) = 5, and the cores in the third stack of four are in the conditions 0, 1, 1, 0, corresponding to (0 + 2 + 4 + 0) = 6. The three stacks together, therefore, are storing the number 956. The three stacks of four cores shown can thus store any number between 0 and 999, that is to say any three-figure number. Clearly, in order to store any four-figure number, four elements will be required in each matrix plane, and to store any number comprised of n digits, n elements will be required in each matrix plane, or 4 × n elements in the stack of four planes.
Similarly, it is usually required to store more than one number, so that if the memory is to be capable or storing a maximum of m different numbers each having a maximum of n digits, each matrix plane must contain m × n cores, and the stack of four planes will contain 4 × m × n cores in all. For example, a stack of four matrix planes, each like that shown in Fig. 7, would be capable of storing up to four numbers, each consisting of up to five digits (or, alternatively, five numbers, each consisting of four digits).

The process of storing or memorising information, in this case a binary-coded decimal figure, is termed ‘writing-in’. It is now necessary to explain in rather more detail how this is carried out.
It is done with the aid of three of the four wires which are threaded through the ring cores. These are the Y-wire, the X-wire and the Z-wire. The Y-wire is so arranged that it passes through each core in the stack of four in one direction; the X-wire passes through each core in the stack of four at right angles to the Y-wire, and the Z-wire passes through each core in a particular matrix plane in the same direction as the X-wires (see Fig. 11). We will take as an example, the process of writing in the decimal digit 9 which, as we have already seen, is represented in the binary code by a stack of four cores magnetised in the sequence 1, 0, 0, 1.
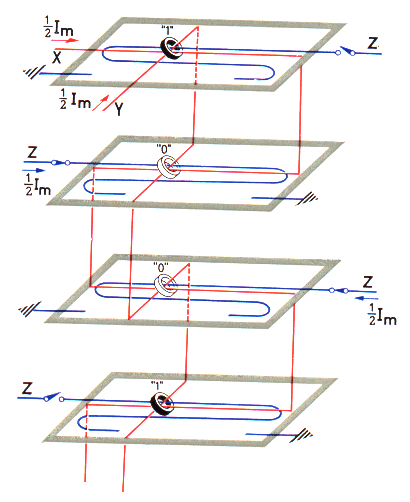
Fig. 11 shows diagrammatically the stack of four cores, one on each of four matrix planes, which is to be brought into the conditions 1, 0, 0, 1, together with the X- and Y-wires and the four Z-wires. It should be noted that each Z-wires, one for each matrix plane, is controlled by a separate switching device.
Starting with all four of the cores concerned in the 0 condition, if current pulses equivalent to a magnetising field of +½H are passed simultaneously through the X- and Y-wires, all four cores would change to the 1 condition. But in order to write in the digit 9, it is necessary that the two centre cores shall remain in the ‘0’ condition. This is achieved by passing at the same time a current pulse corresponding to a field of -½H through the Z- (or ‘inhibit’) wires of the two centre planes. This is shown in the diagram by the positions of the Z-switches.
It will thus be clear that the top and bottom cores of the stack of four are subjected to a field of +½H by the Y-wire and a field of +½H by the X-wire, making a total of (+½H) + (+½H) = H, and will therefore change to condition 1, while the two centre cores are subjected to a field of +½H by the Y-wire, a field of +½H by the X-wire, and a field of -½H by the Z-wires, making a total of (+½H) + (+½H) + (-½H) = +½H only, so that they will not change from their original 0 condition.
The process of recalling information stored in a memory is termed ‘reading-out’. It consists essentially of producing an electrical signal corresponding to the signal which originally supplied the information.
It is achieved, as in the case of ‘writing-in’, with the aid of three wires, but this time the X- and Y-wires and the S-(or ‘sensing’) wire. It will be remembered that the S-wire passes diagonally through every ring core of a matrix plane. A separate S-wire is provided for every plane.
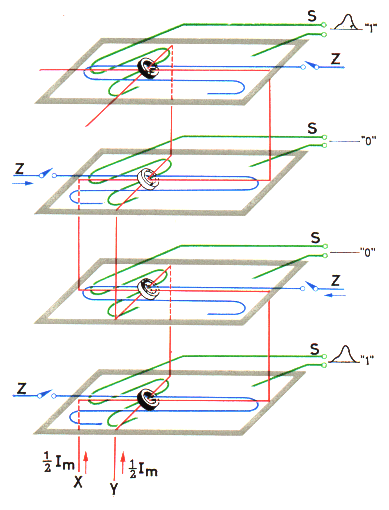
Fig. 12 again shows a set of four matrix planes with their associated wires, and a selected stack of four core elements, one on each plane, magnetised in the sequence 1, 0, 0, 1 representing the symbol 9.
The process of reading-out is based upon the fact that, just as suitable current pulses applied via the X- and Y-wires can change the magnetisation of a core, so a change in the magnetisation of that core produces an electrical pulse in the S-wire threaded through that core. To read out a figure, therefore, current pulses corresponding to a field of -½H are passed through both the X-wires and the Y-wires of the selected stack. All cores are thus subjected to a field of (-½H) + (-½H) = -H. Those cores which were originally in the 1 condition therefore immediately change to the 0 condition, and in so doing induce electrical pulses in the S-wire of the corresponding matrix plane. Those cores which are already in the 0 condition, however, change their magnetisation only slightly, and thus produce only a small electrical pulse.
Once the stored information is read out in this way, that information is lost, that is to say it no longer remains in the memory. However, the electronic equipment can be so designed that as the information is read out it is immediately written back and stored afresh, so that it is once more available for further operations.
Fig. 13 shows how the ring cores of a matrix plane are arranged in practical memories, and how the Y-, X-, Z- and S-wires are threaded through them. The alternate orientation of the cores has been adopted to facilitate construction, since it permits the Z-wire to be threaded to-and-fro along the rows, and the S-wire to be threaded diagonally through all the cores in the matrix plane in such a way that the small ‘interference’ pulses generated by the half-selected cores are cancelled out.
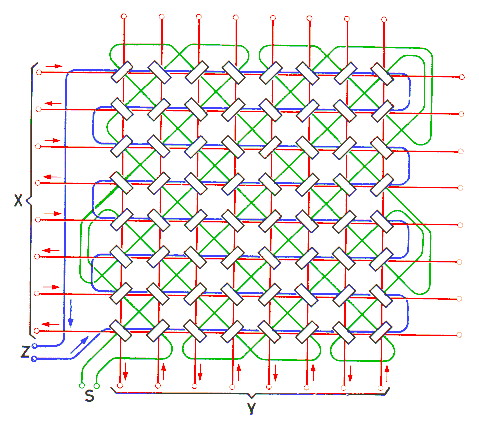
This arrangement of the cores makes it necessary that the ‘write’ current pulses in adjacent X-wires and Y-wires of a matrix plane shall flow in opposite directions, as indicated by the arrows, to ensure that in each core the pulse in the Z-wires opposes those in the X-wire and Y-wire.
A very convenient size of memory plane has 64 rows each containing 64 cores. In large memories stacks of up to 100 such planes are employed. A number of different types of core are available, the choice of the type to be used in the several matrix planes depending upon the time required for a complete read-write cycle.